1級建築施工管理技士 過去問
令和7年(2025年)
問2 (午前 イ 問2)
問題文
ただし、点光源の配光特性は一様なものとし、床面、天井面、壁面等からの反射は考慮しないものとする。
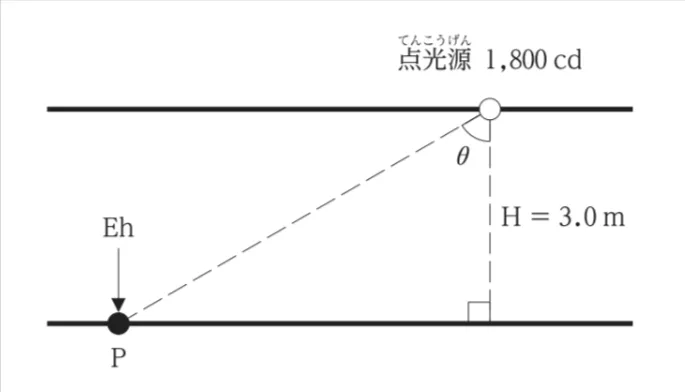
「照明による受照面の明るさを表す照度は、点光源の光度に比例し、その光源からの距離の2乗に反比例する。図に示すような点光源の直下ではない床面上の点Pの水平面照度Ehは、照度の余弦則を用いて計算することができ、点光源の点Pに対する入射角θを60°とした場合、その値は( )lx(クルス)となる。」
このページは閲覧用ページです。
履歴を残すには、 「新しく出題する(ここをクリック)」 をご利用ください。
問題
1級建築施工管理技士試験 令和7年(2025年) 問2(午前 イ 問2) (訂正依頼・報告はこちら)
ただし、点光源の配光特性は一様なものとし、床面、天井面、壁面等からの反射は考慮しないものとする。
「照明による受照面の明るさを表す照度は、点光源の光度に比例し、その光源からの距離の2乗に反比例する。図に示すような点光源の直下ではない床面上の点Pの水平面照度Ehは、照度の余弦則を用いて計算することができ、点光源の点Pに対する入射角θを60°とした場合、その値は( )lx(クルス)となる。」

- 25
- 50
- 150
- 260
正解!素晴らしいです
残念...

この過去問の解説 (2件)
01
点光源の直下ではない床面上の点における、水平面照度を求める問題です。
問題文にあるとおり、「照度の余弦則」を用いて求めることができますが、先に必要な数値を計算していきます。
・点光源~点Pまでの距離(R)=点光源、点P、さらに点光源より垂直に水平面までおろした点をOとし、3点を結んだ三角形に三平方の定理を当てはめると、
H:R:PO=1:2:√3となり、R=6.0mと求められます。
ここで「照度の余弦則」に代入していきます。
Eh〔lx〕=I〔cd〕cosθ/R〔m〕²=1,800×0.5/36=25〔lx〕
以上で、水平面の照度を求めることができます。
正です。解説は上記の通りとなります。
誤です。解説は上記の通りとなります。
誤です。解説は上記の通りとなります。
誤です。解説は上記の通りとなります。
公式自体は難しくありませんが、正しい数値を計算するために、公式に代入するものの確認をしておきましょう。
参考になった数18
この解説の修正を提案する
02
答えは「25」lx(クルス)です
点光源の照度は、距離の2乗に反比例(逆二乗則)し、
床のような水平面では余弦則(よげんそく)(入射角によって暗くなる)も掛けて求めます。
高さH=3.0m、入射角θ=60°なので、光源から点Pまでの距離rは
r=H÷cosθ=3.0÷0.5=6.0m
光の進む方向に直角な面での照度は
E0=I÷r^2=1800÷6^2=1800÷36=50lx
床(水平面)の照度Ehは、余弦則でさらにcosθを掛けます
Eh=E0×cosθ=50×0.5=25lx
したがって25lxになります。
この問題は、次の2つをセットで使うのがポイントです。
・逆二乗則:Eは距離rの2乗で小さくなる(I÷r^2)
・余弦則:水平面ではcosθを掛けてさらに小さくなる(×cosθ)
今回のように、θが大きい(60°)と、距離が伸びるうえに余弦則でも暗くなるため、結果は25lxのように小さくなります。
参考になった数12
この解説の修正を提案する
前の問題(問1)へ
令和7年(2025年) 問題一覧
次の問題(問3)へ